Question

A rectangular painting has dimensions x + 8. The painting has a frame that is 3 inches wide. The total area of the picture and the frame is 384 inches ^2. Find the dimensions of the painting in inches.

1) None of the choices are correct.
2) x² + 20x + 84 = 384
3) x² + 13x + 33 = 384
4) x² + 13x - 351 = 0

Answer 1

`x^2+20x+84=384`

The dimensions of the painting are 10 in by 18 in

Explanation:

The complete question is

A rectangular painting has dimensions x and x + 8. The painting has a frame that is 3 inches wide. The total area of the picture and the frame is 384 inches ^2. Find the dimensions of the painting in inches

we know that

The area of the painting is

`x(x+8)`

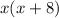
The total area of the picture and the frame is 384 inches ^2

so

`(x+3+3)(x+8+3+3)=384`

`(x+6)(x+14)=384`

`x^2+14x+6x+84=384`

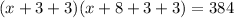
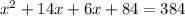
`x^2+20x+84=384` ----> correct choice

solve the quadratic equation by graphing

`x^2+20x-300=0`

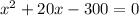
using a graphing tool

The solution is x=10 in

see the attached figure

therefore

The dimensions of the painting are 10 in by 18 in