Question

When the area in square units of an expanding circle is increasing twice as fast as its radius in linear units, the radius is...?

(a) \frac{1}{4\Pi }
(b) \frac{1}{4}
(c) \frac{1}{\Pi }
(d) 1
(e) \Pi

Answer 1

c.
`(1)/(\pi)`

Explanation:

We have been given that the area in square units of an expanding circle is increasing twice as fast as its radius in linear units

We will use derivatives to solve our given problem.

We know that area (A) of a circle is equal to
`A=\pi r^2`.

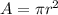Let us find derivative of area function with respect to time.

`(dA)/(dt)=(d)/(dt)(\pi r^2)`

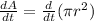
Bring out constant:

`(dA)/(dt)=\pi (d)/(dt)(r^2)`

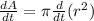
Using power rule and chain rule, we will get:

`(dA)/(dt)=\pi(2r)* (dr)/(dt)`

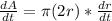
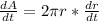`(dA)/(dt)=2\pi r*(dr)/(dt)` Here
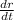`(dr)/(dt)` represents change is radius with respect to time.

We have been given that area of an expanding circle is increasing twice as fast as its radius in linear units. We can represent this information in an equation as:

`(dA)/(dt)=2(dr)/(dt)`

`2\pi r* (dr)/(dt)=2(dr)/(dt)`

`2\pi r=2`

`(2\pi r)/(2\pi)=(2)/(2\pi)`

`r=(1)/(\pi)`

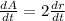
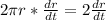
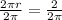
Therefore, the radius is
`(1)/(\pi)` and option 'c' is the correct choice.

Answer 2

This kind of question is solved by using derivatives

Solution:

r = 1/π

The area of a circle is: Ac = π×r² where r is the radius of the circle

If this area is expanding that mean Ac and r are a function of time and the speed is dA/dt and dr/dt can be found from the equation of the area

Then:

Ac = π×r²

dA/dt = 2×π×r×dr/dt

According to the problem statement

dA/dt = 2×dr/dt

By substitution

2×dr/dt = 2×π×r×dr/dt

Simplifying

1 = π×r

and

r = 1/π