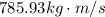Question

An animal-rescue plane flying due east at 27 m/s drops a bale of hay from an altitude of 74 m . The acceleration due to gravity is 9.81 m/s 2 . If the bale of hay weighs 165 N , what is the momentum of the bale the moment it strikes the ground? Answer in units of kg m/s.

Answer 1

To solve this problem we will find the net speed, through the two components given. The vertical component will be found through the energy conservation theorem. Finally with speed we will find the momentum as a function of mass and speed. Given the weight we will divide it by the acceleration to find that mass.

The x component is given as

`v_x = 27m/s`

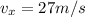
For conservation of energy the vertical component of velocity would be

`PE = KE`

`mgh = (1)/(2) mv_y^2`

`v_y = √(2gh)`

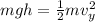
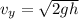
Here,

m = Mass

g = Gravitational acceleration

h = Height

Replacing we have that the vertical velocity is

`v_y = √(2(9.8)(74))`

`v_y = 38.08m/s`

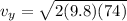
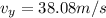
The magnitude of this velocity would be

`|V| = √(v_x^2+v_y^2)`

`|V| = √(27^2+38.08^2)`

`|V| = 46.68m/s`

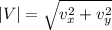
Finally the momentum of the bale would be

`p = mv`

`p = ((F)/(g))(v)`

`p = ((165)/(9.8))(46.68)`

`p = 785.93kg\cdot m/s`

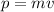
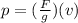
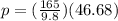
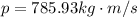
Therefore the momentum of the bale the moment it strikes the ground is
`785.93kg\cdot m/s`