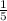The probability that a student took either tech or foods is
Solution:
In a poll of 20 high school seniors, 7 took a tech class and 12 took a foods class
3 students took both tech and foods
Therefore,
Total number of students = 20
Number of students took tech class alone = 7 - 3 = 4
Number of students took food class alone = 12 - 3 = 9
Number of students both class = 3
Thus,
Number of students took either tech or food = Total number of students - (Number of students took tech class alone + Number of students took food class alone + Number of students both class)
Number of students took either tech or food = 20 - (4+9+3)
Number of students took either tech or food = 20 - 16 = 4
To find: probability that a student took either tech or foods
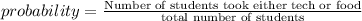
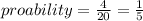
Thus probability that a student took either tech or foods is