Five sales men could sell 18 cars
Solution:
The number of cars sold is proportional to the number of salesmen

Let "c" be the number of cars sold
Let "s" be the number of salesmen
Then we get,
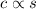
c = ks -------- eqn 1
Where "k" is the constant of proportionality
Three salesmen sold eleven cars
Therefore, substitute s = 3 and c = 11 in eqn 1
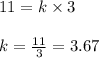
How many could five salesmen have sold ?
Therefore, s = 5 and c = ?
Substitute s = 5 and k = 3.67 in eqn 1
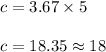
Thus five men sold 18 cars