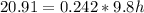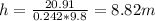Answer:
8.82 m
Step-by-step explanation:
When compressed, the spring potential energy is:
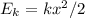
where k = 5050 N/m is the spring constant, x = 0.091 is the distance compressed

This energy would be converted to kinetic, so the mass gains speed, which is then converted to gravitational potential energy once the mass reaches its highest point, which is 0 speed/kinetic energy
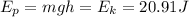
where m = 0.242 kg is the mass of the block, g = 9.8m/s2 is the gravitational acceleration, and h is the maximum height which we are looking for