Question

Determine whether rolle's theorem can be applied to the function f(x) = x(x-2)^2 from 0 to 2

Answer 1

Rolle's theorem can be applies over the interval [0,2] for the given function f(x).

Explanation:

We are given the following in the question;

`f(x) = x(x-2)^2 \text{ in }[0,2]`

The Rolle's theorem states that is

1. f(x) is continuous on the interval [a,b]
2. f(x) is differentiable on the interval (a,b)
3. f(a) = f(b)

then, there exist c in the interval (a,b) such that

`f'(c) = 0`

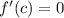
Condition:

Continuity of f(x)

Since f(x) is a polynomial function, it is continuous i the given interval [0,2].

Differentiability of f(x)

Since f(x) is a polynomial function, it is continuous i the given interval (0,2).

Equality of f(x)

`f(0) = 0(0-2)^2 = 0\\f(2) = 2(2-2)^2 = 0\\f(0) = f(2)`

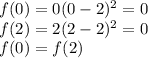
Thus, Rolle's theorem can be applies over the interval [0,2] for the given function f(x).