Question

Which equation is the inverse of y = 2x2 – 8? y = plus-or-minus StartRoot StartFraction x + 8 Over 2 EndFraction EndRoot y = StartFraction plus-or-minus StartRoot x + 8 EndRoot Over 2 EndFraction y = plus-or-minus StartRoot StartFraction x Over 2 EndFraction + 8 EndRoot y = StartFraction plus-or-minus StartRoot x EndRoot Over 2 EndFraction + 4

Answer 1

Answer: A

Step-by-step explanation: No cap

Answer 2

y = plus-or-minus StartRoot StartFraction x + 8 Over 2 EndFraction EndRoot

`y=\pm\sqrt{(x+8)/(2)}`

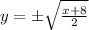
Explanation:

Given:

The equation to find inverse is given as:

`y=2x^2-8`

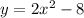
In order to find the inverse, we apply the following steps.

Step 1: Switch 'y' with 'x' and 'x' with 'y'. Thi gives,

`x=2y^2-8`

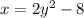
Step 2: Now, again rewrite the above equation in terms of 'y'.

Adding 8 on both sides, we get:

`x+8=2y^2-8+8`

`x+8=2y^2`

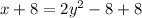
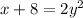
Now, rewriting 'y' terms on the left side of the equation, we get

`2y^2=x+8`

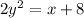
Dividing both sides by 2, we get:

`(2y^2)/(2)=(x+8)/(2)\\\\y^2=(x+8)/(2)`

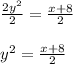
Taking square root on both sides, we get:

`√(y^2)=\pm\sqrt{(x+8)/(2)}\\\\y=\pm\sqrt{(x+8)/(2)}`

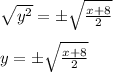
Thus, the inverse of the given equation is
`y=\pm\sqrt{(x+8)/(2)}`.

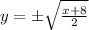So, the first option is correct.