Answer:
23.63 m/s
Step-by-step explanation:
We can assign the bottom of the hill to have zero potential energy.
Thus, the car has only potential energy at the top of the hill.
At the bottom of the hill, all of the potential energy is converted into kinetic energy.
Therefore, initial potential equals final kinetic:

Substitute:
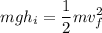
Solve for final velocity:
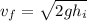
Therefore, the velocity of the car at the bottom of the hill is:
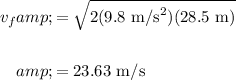
In conclusion, the velocity of the car at the bottom of the hill is about 23.63 m/s.