Question

A rectangle is constructed on a semicircle so that the length equals the diameter. The rectangle is 3 times as long as it is wide. The total area of the figure is 750 in.2. Find the approximate dimensions of the rectangle.

Answer 1

Length of the rectangle = 32.14 inches

Width of the rectangle = 10.71 inches

Explanation:

Given:

The rectangle is 3 times as long as it is wide

total area of the figure = 750 in.2

To Find:

dimensions of the rectangle = ?

Solution:

The area of the figure = Area of the rectangle + Area of semicircle

Rectangle is 3 times as long as it is wide

Let r be the radius of the semicircle

Then

Length = 2r

Width =
`(2r)/(3)`

The area of the figure =
`(2r * (2r)/(3)) * ((\pi r^2)/(2))`

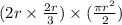
750 =
`((4r^2))/(3) + (\pi r^2)/(2)`

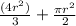
750 =
`r^2((4)/(3) +(\pi)/(2))`

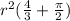
750 =
`r^2(1.33+1.57)`

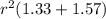
750 =
`r^2(2.9)`

`(750)/(2.9) = r^2`

`258.6 = r^2`

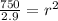
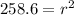
r = 16.07

Then diameter d = 2(r) = 2(16.07) = 32.14

Now

length of the rectangle = 2r = 32.14 inches

Width =
`(2r)/(3)`=
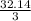`(32.14)/(3)`= 10.71 inches