Question

M+1 3/8=5 What does m equal?

Answer 1

`\text{ The value of m is equal to 3.625 or }(29)/(8) \text{ or } 3(5)/(8)`

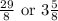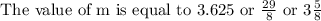
Solution:

Given that we have to find the value of "m"

Given expression is:

`m + 1(3)/(8) = 5`

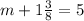
Let us first convert the mixed fraction to improper fraction

Steps to follow:

Divide the numerator by the denominator.

Write down the whole number answer.

Then write down any remainder above the denominator.

Therefore,

`1(3)/(8)=(8 * 1+3)/(8) = (8+3)/(8) = (11)/(8)`

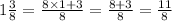
Now the expression becomes,

`m + (11)/(8) = 5`

Keep the variable "m" on L.H.S and move the constant to R.H.S

`m = 5 - (11)/(8)\\\\m = (5 * 8 -11)/(8)\\\\m = (40-11)/(8)\\\\m = (29)/(8)\\\\\text{In mixed fractions, we can write as }\\\\m = (29)/(8) = 3(5)/(8)`

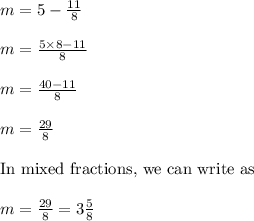
Thus value of m is equal to 3.625 or
`(29)/(8) \text{ or } 3(5)/(8)`