Answer:
651 is the minimum number of people over age 30 they must include in their sample.
Explanation:
We are given the following information:
Confidence level = 90%
Significance level = 10%
Maximum error = 0.09
Variance = 1.96
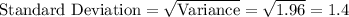
Formula:
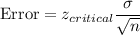
Putting all the values,
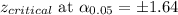
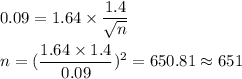
651 is the minimum number of people over age 30 they must include in their sample.