Answer:
remaining factors: (x +1)(x² +2x +3)
Explanation:
Synthetic division can be used to divide the given polynomial by the given factor. The result is ...
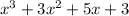
We observe there are no changes in sign here, so the factor (x-1) represents the only positive real root. When we change the signs of the odd-degree terms, we now have 3 sign changes, indicating 3 or 1 negative real roots. We also observe that the sign-altered coefficients sum to zero, meaning that x=-1 is a real root of the polynomial.
At this point, we know a second factor is (x+1). Again using synthetic division, we find the remaining factor is a quadratic with no real roots:
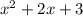
__
The remaining factors (after (x-1)) with real coefficients are ...
(x +1)(x² +2x +3)
_____
The quadratic can be factored in the complex numbers as ...
(x +1 -i√2)(x +1 +i√2)
_____
Comment on sign changes
The discussion of sign changes refers to Descartes' rule of signs. It says the number of positive real roots is equal to the number of changes of sign of the coefficients when the polynomial is written in standard form. That number may be reduced by multiples of 2 if some of the roots are complex.
Hence the 3 sign changes we observe in -x^3 +3x^2 -5x +3 means there are either 3 or 1 negative real roots. (If f(x) has negative real roots, f(-x) will have positive real roots.)
__
Comment on the graph
For higher-degree polynomials, I like to see what information a graphing calculator can provide about roots. Here, it tells us the real roots are -1 and +1 and the other two roots are complex. Factoring out the factors related to the real roots gives the quadratic (x+1)^2 +2 = x^2 +2x +3, as above. The vertex of the quadratic gives useful information about the complex roots.