Question

A cone-shaped coffee filter of radius 6 cm and depth 10 cm contains water, which drips out through a hole at the bottom at a constant rate of 1.5 cm3 per second. (a) If the filter starts out full, how long does it take to empty

Answer 1

It takes 251.33 seconds to filter out full.

Explanation:

We are given the following in the question:

Radius of cone, r = 6 cm

Depth of cone,h = 10 cm

Volume of flow rate =

`(dv)/(dt) = 1.5~ cm^3/s`

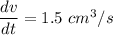
Volume of cone-shaped coffee filter =

`(1)/(3)\pi r^2 h`

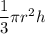
The volume of the cone when water start drips out =

`(1)/(3)\pi r^2 h - 1.5t`

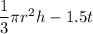
Since, when the cone will be empty the volume of cone will be zero, thus we can write,

`0 = (1)/(3)\pi r^2 h - 1.5t`

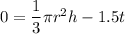
Putting all the values, we get,

`0 = (1)/(3)\pi (6)^2 (10) - 1.5t\\\\t = (1)/(1.5)* (1)/(3)(3.14)(6)^2(10)\\\\t = 251.33 \text{ seconds}`

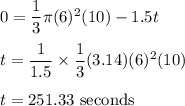
Thus, it takes 251.33 seconds to filter out full.