Question

Assume the exponential growth model ​A(t)equals=Upper A 0 e Superscript ktA0ekt and a world population of 5.95.9 billion in 20062006. If the population must stay below 2424 billion during the next 100​ years, what is the maximum acceptable annual rate of​ growth?

Answer 1

1.4% is the maximum acceptable annual rate of​ growth such that the population must stay below 24 billion during the next 100​ years.

Explanation:

We are given the following in the question:

The exponential growth model ​is given by:

`A(t) = A_0e^(kt)`

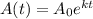
where k is the growth rate, t is time in years and
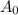`A_0` is constant.

The world population is 5.9 billion in 2006.

Thus, t = 0 for 2006

`A_0 = 5.9\text{ billions}`

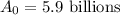
We have to find the maximum acceptable annual rate of​ growth such that the population must stay below 24 billion during the next 100​ years.

Putting these values in the growth model, we have,

`24 = 5.9e^(100k)\\\\k = (1)/(100)\ln \bigg((24)/(5.9)\bigg)\\\\k = 0.01403\\k = 0.01403* 100\% = 1.4\%`

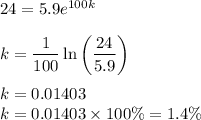
1.4% is the maximum acceptable annual rate of​ growth such that the population must stay below 24 billion during the next 100​ years.