Question

HELP NOW Choose all that give the correct equation of the line parallel or perpendicular to the given line passing through the point. The line y = 7 5 x + 4 passing through the point (5, 2) is parallel to the line y = 7 5 x − 5. The line −x + y = −1 passing through the point (1, −5) is perpendicular to the line y = −x − 4. The line y = 9 2 x − 5 passing through the point (3, 4) is perpendicular to the line y = 9 2 x − 19 2 . The line 3x + 7y = 0 passing through the point (−3, −5) is parallel to the line y = 7 3 x + 2.

Answer 1

A and B

Explanation:

The line y = 7/5 x + 4 passing through the point (5, 2) is parallel to the line y = 7 /5x − 5.

and

The line −x + y = −1 passing through the point (1, −5) is perpendicular to the line y = −x − 4.

Answer 2

Neither of the options are correct.

Explanation:

Option A :

Line parallel to the equation
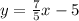`y = (7)/(5)x - 5` will have equation

`y = (7)/(5)x + c` ........... (1)

If it passes through the point (5,2) then this will satisfy the equation (1).

Hence,
`2 = (7)/(5) * 5 + c`

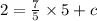
⇒ c = - 5

So, the equation (1) becomes
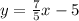`y = (7)/(5)x - 5` (Answer)

Option B :

Line perpendicular to the equation y = - x - 4 will have equation - x + y = c ........... (2)

{Because slope of the original line is - 1 and that of the perpendicular line is 1 and hence the product is (- 1) × (1) = - 1}

Now, if the equation (2) passes through the point (1,-5), then we get,

- 1 + (- 5) = c

⇒ c = - 6

Therefore, the equation (2) becomes, -x + y = - 6. (Answer)

Option C :

Line perpendicular to the equation
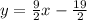`y = (9)/(2) x - (19)/(2)` will have equation
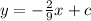`y = - (2)/(9)x + c` ........... (3)

{Because slope of the original line is
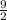`(9)/(2)` and that of the perpendicular line is
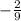`- (2)/(9)` and hence the product is (
`(9)/(2)`) × (
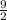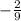`- (2)/(9)`) = - 1}

Now, if the equation (3) passes through the point (3,4), then we get,

`4 = - (2)/(9)* 3 + c`

⇒
`c = (14)/(3)`

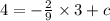
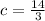
Therefore, the equation (3) becomes,
`y = - (2)/(9)x +  (14)/(3)`. (Answer)

Option D :

Line parallel to the equation
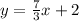`y = (7)/(3)x + 2` will have equation

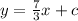`y = (7)/(3)x + c` ........... (4)

If it passes through the point (-3,-5) then this will satisfy the equation (1).

Hence,
`- 5 = (7)/(3) * (-3) + c`

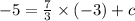
⇒ c = 2

So, the equation (1) becomes
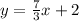`y = (7)/(3)x + 2` (Answer)

Therefore, neither of the options are correct. (Answer)