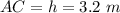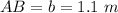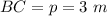Question

The hypotenuse of a right triangle is 1 meter longer than twice the length of one leg. If the other leg is measures 3 meters find the lengths of each unknown side to the nearest tenth of a meter.

Answer 1

`AC= h = 3.2\ m`

`AB= b = 1.1\ m`

`BC= p = 3\ m`

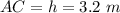
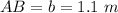
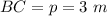
Explanation:

Let x be the length of the one side of a right angle triangle.

Given:

The hypotenuse of a right triangle is 1 meter longer than twice the length of one leg, and the length of the other leg measure 3 meters.

Length of one leg b = x

So length of the hypotenuse h = 2x + 1

Length of other leg p = 3 m

We need to find the length of each unknown side.

Solution.

From the figure h is the length of the hypotenuse AC and b, p is length of the legs AB and BC

Using Pythagoras theorem.

`(AC)^(2) = (AB)^(2)+(BC)^(2)`

`h^(2) = (b)^(2)+(p)^(2)`

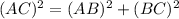
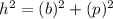
Substitute all given value in above equation and then simplify.

`(2x+1)^(2) = x^(2)+(3)^(2)`

`4x^(2)+1+4x= x^(2)+9`

`4x^(2)-x^(2)-9+1+4x= 0`

`3x^(2)+4x-8 = 0`

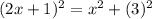
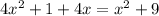
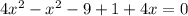
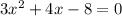
Now, we first find the root of the above equation.

Use quadratic formula with
`a=3, b=4, c=-8`.

`x=\frac{-b\pm \sqrt{(b)^(2)-4ac}}{2a}`

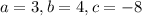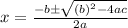
Put a, b and c value in above equation.

`x=\frac{-4\pm \sqrt{(4)^(2)-4(3)(-8)}}{2(3)}`

`x=(-4\pm √(16+96))/(6)`

`x=(-4\pm √(112))/(6)`

`x=(-4\pm 4√(7))/(6)`

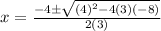
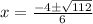
For positive sign

x = 1.1 m

So the length of the hypotenuse
`h = 2x+1`

`h = 2* 1.1+1`

`h = 2.2+1`

`h = 3.2\ m`

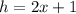
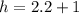
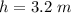
Therefore, the length of the each side of the right angle triangle is given below.

`AC= h = 3.2\ m`

`AB= b = 1.1\ m`

`BC= p = 3\ m`