Question

A group issimpleif it has no nontrivial proper normal subgroups. LetGbe a simple group of order168. How many elements of order 7 are there inG

Answer 1

6*8=48 groups with elements of order 7

Explanation:

For this case the first step is discompose the number 168 in factors like this:

`168 = 8*3*7= 2^3 *3*7`

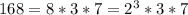
And for this case we can use the Sylow theorems, given by:

Let G a group of order
`p^(\alpha) m` where p is a prime number, with
`m\leq 1` and p not divide m then:

1)
`Syl (G) \\eq \emptyset`

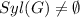
2) All sylow p subgroups are conjugate in G

3) Any p subgroup of G is contained in a Sylow p subgroup

4) n(G) =1 mod p

Using these theorems we can see that 7 = 1 (mod7)

By the theorem we can't have on one Sylow 7 subgroup so then we need to have 8 of them.

Every each 2 subgroups intersect in a subgroup with a order that divides 7. And analyzing the intersection we can see that we can have 6 of these subgroups.

So then based on the information we can have 6*8=48 groups with elements of order 7 in G of size 168