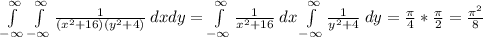Answer:
Explanation:
We are given the following improper integral:
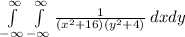
Above double integral can be written as follows:
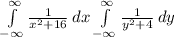
When we have improper integral with two infinite bounds, we are separating them into two parts.
So let's calculate them one by one.
First,
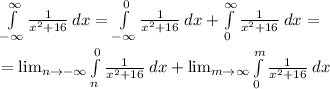
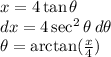
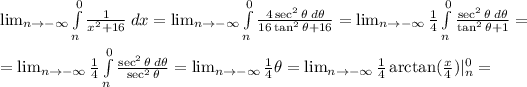
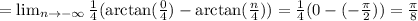
Since,
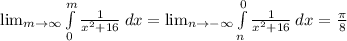
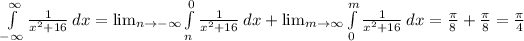
Second,
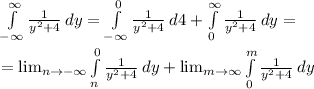
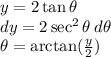
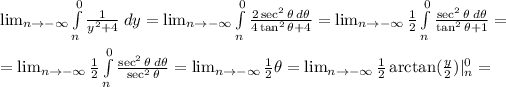
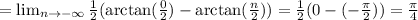
Since,
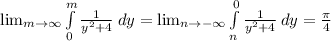
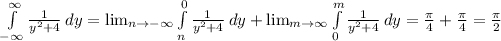
Hence,