Question

Differentiating a Logarithmic Function in Exercise, find the derivative of the function. See Examples 1, 2, 3, and 4.

f(x) = 2x ln x

Answer 1

`(df(x))/(dx)=2(1+lnx)`

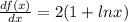
Explanation:

From our knowledge of derivatives we use the product rule approach, the product rule is stated below

For f(x)=u(x)v(x) the derivative is express as

`(df(x))/(dx)=u(x)(dv(x))/(dx)+v(x)(du(x))/(dx)\\`

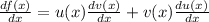
hence from the question f(x)=2xlnx,

we can assign u(x)=2x and v(x)=lnx

also the derivative of u(x)=2x is simply

`(du(x))/(dx)=2`

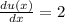
and the derivative of v(x)=lnx can be express using the general log derivative i.e

`y=lnx\\(dy)/(dx)=(1)/(x) \\`

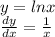
hence we have
`(dv(x))/(dx)=(1)/(x) \\`

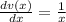
if we substitute value into the general product expression stated earlier we arrive at

`(df(x))/(dx)=2x(1)/(x)+lnx*2\\(df(x))/(dx)=2+2lnx\\(df(x))/(dx)=2(1+lnx)`