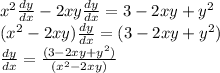Question

In Exercise, find dy/dx implicity.
x2y - xy2 = 3x

Answer 1

`(dy)/(dx) =((3-2xy+y^(2)))/((x^(2)-2xy))`

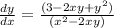
Explanation:

From the equation its is obvious that y is define as an explicit function of x, hence to solve implicitly, we differentiate each term of the equation with respect to x.

`x^(2) y-xy^(2)=3x\\`

`((d(x^(2)))/(dx)y+ (d(y))/(dx)x^(2))-((d(x))/(dx)y^(2) + (d(y^(2) ))/(dx)x)\\(2xy+ (d(y))/(dx)x^(2))-(y^(2) + (d(y^(2) ))/(dx)x)=3\\`

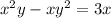
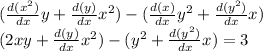
Now
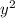`y^(2)` is a function of y which itself is a function of x. Thus by general differentiation we arrive at

`(2xy+x^(2) (dy)/(dx))-(y^(2) +2yx(dy)/(dx))=3\\`

`2xy+x^(2) (dy)/(dx)-y^(2) -2yx(dy)/(dx)=3\\`

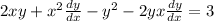
bring similar terms we arrive at

`x^(2) (dy)/(dx) -2xy(dy)/(dx)=3-2xy+y^(2) \\(x^(2)-2xy)(dy)/(dx) =(3-2xy+y^(2))\\(dy)/(dx) =((3-2xy+y^(2)))/((x^(2)-2xy))`