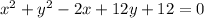Question

Write the equation of a circle for which the endpoints of a diameter are (-2,-2) and (4,-10)

Answer 1

Therefore the required Equation of Circle

`x^(2)+y^(2)-2x+12y+12=0`

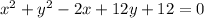
Explanation:

Given:

End point of Diameter be

point A( x₁ , y₁) ≡ ( -2 ,-2 )

point B( x₂ , y₂) ≡ ( 4 , -10 )

To Find:

Equation of a circle =?

Solution:

When end points of the Diameter are A( x₁ , y₁) , B( x₂ , y₂). then the Equation of Circle is given as

`(x-x_(1))(x-x_(2))+(y-y_(1))(y-y_(2))=0`

Substituting the end point are

`(x-(-2))(x-4)+(y-(-2))(y-(-10))=0\\(x+2))(x-4)+(y+2))(y+10))=0\\`

Applying Distributive Property we get

`x^(2) -2x-8+y^(2)+12y+20 =0\\\\x^(2)+y^(2)-2x+12y+12=0`

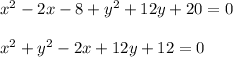
Therefore the required Equation of Circle

`x^(2)+y^(2)-2x+12y+12=0`