Answer:
Explanation:
Given that B is 3x3 matrix.
To prove that B+B^T is symmetry
We know B Transpose matrix will be the matrix got by interchanging the rows and columns of B.
When we interchange rows and columns, we find diagonals remain in the same position
In other words,
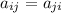 if i =j
if i =j
When we add B with B transpose we add diagonal elements twice
and other elements aij with aji for each of the other entry.
Diagonal elements will not pose a problem now when the sum matrix is transposed
B+BT will have ijth entry as =
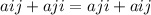
i.e. the matrix have to be symmetrical