Question

Brady made a scale drawing of a rectangular swimming pool on a coordinate grid. The points (-20, 25), (30, 25), (30, -10) and (-20, -10) represent the corners of the pool. What are the dimensions of the pool?

Answer 1

Length = 50 units

width = 35 units

Explanation:

Let A, B, C and D be the corner of the pools.

Given:

The points of the corners are.

`A(x_(1), y_(1)})=(-20, 25)`

`B(x_(2), y_(2)})=(30, 25)`

`C(x_(3), y_(3)})=(30, -10)`

`D(x_(4), y_(4)})=(-20, -10)`

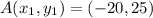
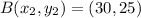
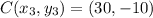
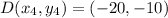
We need to find the dimension of the pools.

Solution:

Using distance formula of the two points.

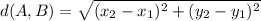`d(A,B)=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)}`----------(1)

For point AB

Substitute points A(30, 25) and B(30, 25) in above equation.

`AB=\sqrt{(30-(-20))^(2)+(25-25)^(2)}`

`AB=\sqrt{(30+20)^(2)}`

`AB=\sqrt{(50)^(2)`

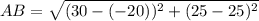
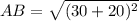
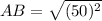
AB = 50 units

Similarly for point BC

Substitute points B(-20, 25) and C(30, -10) in equation 1.

`d(B,C)=\sqrt{(x_(3)-x_(2))^(2)+(y_(3)-y_(2))^(2)}`

`BC=\sqrt{(30-30)^(2)+((-10)-25)^(2)}`

`BC=\sqrt{(-35)^(2)}`

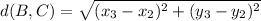
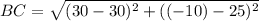
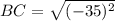
BC = 35 units

Similarly for point DC

Substitute points D(-20, -10) and C(30, -10) in equation 1.

`d(D,C)=\sqrt{(x_(3)-x_(4))^(2)+(y_(3)-y_(4))^(2)}`

`DC=\sqrt{(30-(-20))^(2)+(-10-(-10))^(2)}`

`DC=\sqrt{(30+20)^(2)}`

`DC=\sqrt{(50)^(2)}`

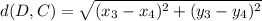
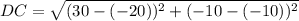
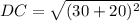
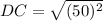
DC = 50 units

Similarly for segment AD

Substitute points A(-20, 25) and D(-20, -10) in equation 1.

`d(A,D)=\sqrt{(x_(4)-x_(1))^(2)+(y_(4)-y_(1))^(2)}`

`AD=\sqrt{(-20-(-20))^(2)+(-10-25)^(2)}`

`AD=\sqrt{(-20+20)^(2)+(-35)^(2)}`

`AD=\sqrt{(-35)^(2)}`

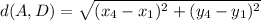
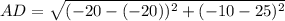
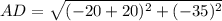
AD = 35 units

Therefore, the dimension of the rectangular swimming pool are.

Length = 50 units

width = 35 units