Question

Differentiating Exponential functions In Exercise,find the derivative of the function. See Example 2 and 3.

f(x) = 2/(e^x + e^-x)3

Answer 1

f'(x) =
`(-6((e^x - e^(-x)))/((e^x + e^(-x))^4)`

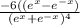
Explanation:

Data provided in the question:

f(x) =
`(2)/((e^x + e^(-x))^3)`

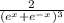
or

we can also write the above equation as:

f(x) = 2 × (eˣ + e⁻ˣ)⁻³

Now,

on differentiating the above equation with respect to 'x', we get

f'(x) = 2 × (-3) × (eˣ + e⁻ˣ)⁻⁴ × (eˣ + (-1)e⁻ˣ)

or

f'(x) =
`(-6((e^x - e^(-x)))/((e^x + e^(-x))^4)`

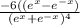
Note: derivative of eˣ = eˣ

derivative of xⁿ = xⁿ⁻¹