Answer:
(a) r = 5.25%,quarterly compounding
Explanation:
We are given the following in the question:
P = $5000
t = 12 months = 1 year
The compound interest is given by
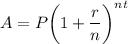
where P is the principal, r is the interest rate, t is the time, n is the nature of compound interest and A is the final amount.
When compounded continuously
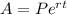
where P is the principal, r is the interest rate, t is the time and A is the final amount.
a) r = 5.25%,quarterly compounding

b) r = 5%,monthly compounding
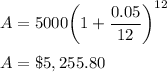
c) r = 4.75%, Continuously compounding

Since, the maximum amount on the principal value is given by r = 5.25%,quarterly compounding