Question

Depreciation A car sells for $28,000.The car

depreciates such that each year it is worth 3/4 of its value from the previous year.Find a model for the value V of the car after t year.Sketch a graph of the model and determine the value of the car 4 years after it is purchased.

Answer 1

`V(t)=28,000(0.75)^t`.

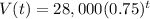$8859.375

Explanation:

Please find the attachment for the function.

We have been given that a car sells for $28,000.The car depreciates such that each year it is worth 3/4 of its value from the previous year. We are asked to find the model for the value V of the car after t years.

We know that an exponential function is in form
`y=a(b)^x`, where,

a = Initial value,

b = Growth or depreciation rate.

Since each year the car worth 3/4 of its value from the previous year, so its value is depreciating and
`b=(3)/(4)=0.75`.

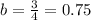Therefore, our required function would be
`V(t)=28,000(0.75)^t`.

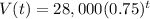To find the value of car after 4 years, we need to substitute
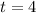`t=4` in our function as:

`V(4)=28,000(0.75)^4`

`V(4)=28,000(0.31640625)`

`V(4)=8859.375`

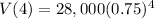
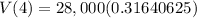
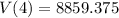
Therefore, the value of the car after 4 years would be $8859.375.