Question

Condensing Logarithmic Expressions In Exercise, use the properties of logarithms to rewrite the expression as the logarithm of a single quantity.

4[In(x3 - 1) + 2 In x - In(x - 5)]

Answer 1

`4ln [(x^2 (x^3-1))/(x-5)]`

Explanation:

For this case we have the following expression:

`4[ln(x^3-1) +2ln(x) -ln(x-5)]`

For this case we can apply the following property:

`a log_c (b) = log_c (b^a)`

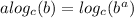
And we can rewrite the following expression like this:

`2 ln(x) = ln(x^2)`

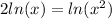
And we can rewrite like this our expression:

`4[ln(x^3-1) +ln(x^2) -ln(x-5)]`

Now we can use the following property:

`log_c (a) +log_c (b) = log_c (ab)`

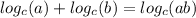
And we got this:

`4[ln(x^3-1)(x^2) -ln(x-5)]`

And now we can apply the following property:

`log_c (a) -log_c (b) = log_c ((a)/(b))`

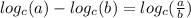
And we got this:

`4ln [(x^2 (x^3-1))/(x-5)]`

And that would be our final answer on this case.