Question

Logarithmic and Exponential Forms of Equations In Exercise, write the logarithmic equation as an exponential equation, or vice versa.

In 0.6 = - 0.5108 ...

Answer 1

`(3)/(5) = e^(-0.5108)`

Explanation:

For this case we have the following expression:

`ln (0.6) = -0.5108`

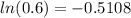
We can rewrite 0.6 like this
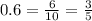`0.6 =(6)/(10)=(3)/(5)` and we have this:

`ln((3)/(5))= -0.5108`

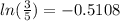
We can rewrite this expression like this:

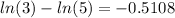`ln (3) -ln(5)= -0.5108`, using properties of logs.
`log_c ((a)/(b))= log_c (a) -log_c (b)`

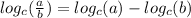
We need to remember that the natural log and the exponentiation with base the euler number e are inverse operations so if we apply esponents on both sides of the equation qe got this:

`(3)/(5) = e^(-0.5108)`

And that would be our final anwer for this case.