Question

Use integration by parts to find the integrals in Exercise.
∫xex dx.

Answer 1

`xe^(x) - e^(x) +C`

Explanation:

using the formular for integration by parts;

∫udv = uv -∫vdu ..............equ 1

in the equation below;

∫
`xe^(x)`

u=x , dv =
`e^(x)`

du= 1 v=
`e^(x)`

Substitute into equ 1

∫udv =
`xe^(x)` - ∫
`e^(x)dx`

∫udv =
`xe^(x)` -
`e^(x) + C`

Answer 2

`\displaystyle \int {xe^x} \, dx = e^x(x - 1) + C`

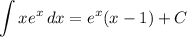
General Formulas and Concepts:

Calculus

Differentiation

• Derivatives
• Derivative Notation

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Integration

• Integrals
• [Indefinite Integral] Integration Constant C

Integration by Parts:
`\displaystyle \int {u} \, dv = uv - \int {v} \, du`

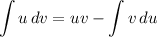
• [IBP] LIPET: Logs, inverses, Polynomials, Exponentials, Trig

Explanation:

Step 1: Define

Identify

`\displaystyle \int {xe^x} \, dx`

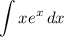
Step 2: Integrate Pt. 1

Identify variables for integration by parts using LIPET.

1. Set u:
   `\displaystyle u = x`
2. [u] Differentiate [Basic Power Rule]:
   `\displaystyle du = dx`
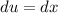
3. Set dv:
   `\displaystyle dv = e^x`
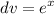
4. [dv] Integrate [Exponential Integration]:
   `\displaystyle v = e^x`

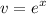
Step 3: Integrate Pt. 2

1. [Integral] Integration by Parts:
   `\displaystyle \int {xe^x} \, dx = xe^x - \int {e^x} \, dx`
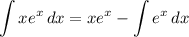
2. [Integral] Exponential Integration:
   `\displaystyle \int {xe^x} \, dx = xe^x - e^x + C`
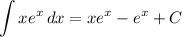
3. Factor:
   `\displaystyle \int {xe^x} \, dx = e^x(x - 1) + C`

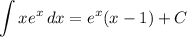
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration