Question

In Exercise, sketch the graph of the function.
f(x) = ln(x – 5)

Answer 1

See the graph and explanation below.

Explanation:

For this case we have the following function:

`f(x) = ln(x-5)`

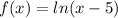
The domain for this function is given by:

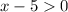`x-5 >0` since the natural log is not defined for negative numbers

`x>5` ,
`D = x \in (5,\infty)`

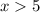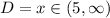
We can calculate some points in order to see the tendency of the graph, we can select a set of points for example
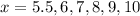`x =5.5, 6,7,8,9,10` and we can calculate the values for f(x) like this

x=5.5

`f(x=5.5) = ln(5.5-5) = ln(0.5) =-0.693`

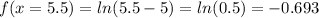
x=6

`f(x=6) = ln(6-5) = ln(1) =0`

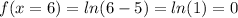
That represent the x intercept

x=7

`f(x=7) = ln(7-5) = ln(2) =0.693`

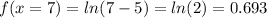
x=8

`f(x=8) = ln(8-5) = ln(3) =1.099`

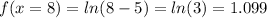
x=9

`f(x=6) = ln(9-5) = ln(4) =1.386`

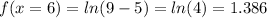
x=10

`f(x=10) = ln(10-5) = ln(5) =1.609`

And that represent the x intercept

And then we can see the plot on the figure attached.