Question

Population Growth The resident populations P (in thousands) of Wisconsin fron 2000 through 2009 can be modeled by the exponential function

P(t) = 5382(1.0057)t
where t is the time in years with t = 0 corresponding to 2000.Use the model to estimate the population in the year (a) 2016 and (b) 2025.

Answer 1

(a) 5894 thousand

(b) 6204 thousand

Explanation:

Given:

The expression for population growth of the residents of Wisconsin is given as:

`P(t)=5382(1.0057)^t`

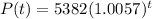
For the year 2000, the time is,
`t=0`

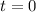
(a) Population in 2016.

Difference in years from 2000 to 2016 = 2016 - 2000 = 16 years.

Therefore, the time 't' for 2016 is equal to 16 years.

Now, plug in 16 for 't' in the above expression and solve for population 'P'. This gives,

`P(t)=5382(1.0057)^t`

`P(16)=5382(1.0057)^(16)\\\\P(16)=5894.4\approx 5894\ thousands`

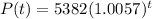
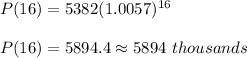
Therefore, the estimated population of the residents in 2016 is 5894 thousand.

(b) Population in 2025.

Difference in years from 2000 to 2025 = 2025 - 2000 = 25 years.

Therefore, the time 't' for 2025 is equal to 25 years.

Now, plug in 25 for 't' in the above expression and solve for population 'P'. This gives,

`P(t)=5382(1.0057)^t`

`P(25)=5382(1.0057)^(25)\\\\P(25)=6203.8\approx 6204\ thousands`

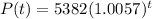
Therefore, the estimated population of the residents in 2016 is 6204 thousand.