Question

Find the area between the graph of the function and the x-axis over the given interval, if possible.

f(x) = 5/(x-2)^2 for (-[infinity], 1)

Answer 1

`A= -(5)/(-1) - \lim_(x\to\infty) (5)/(x-2) = 5-0 = 5`

So then the integral converges and the area below the curve and the x axis would be 5.

Explanation:

In order to calculate the area between the function and the x axis we need to solve the following integral:

`A = \int_(-\infty)^1 (5)/((x-2)^2)`

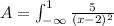
For this case we can use the following substitution
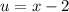`u = x-2` and we have
`dx = du`

`A = \int_(a)^b (5)/(u^2) du = 5\int_(a)^b u^(-2)du`

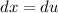
And if we solve the integral we got:

`A= -(5)/(u) \Big|_a^b`

And we can rewrite the expression again in terms of x and we got:

`A = -(5)/(x-2) \Big|_(-\infty)^1`

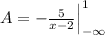
And we can solve this using the fundamental theorem of calculus like this:

`A= -(5)/(-1) - \lim_(x\to\infty) (5)/(x-2) = 5-0 = 5`

So then the integral converges and the area below the curve and the x axis would be 5.