Answer:
A.) After adding 4 to both sides, the equation is
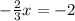
C.) The equation can be solved for x using exactly one more step by multiplying both sides by
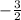
D.) The equation can be solved for x using exactly one more step by dividing both sides by

Explanation:
The correct questions is as follows:
Carina begins to solve the equation -4-2/3x=-6 by adding 4 to both sides. Which statements regarding the rest of the solving process could be true? Check all that apply.
A.) After adding 4 to both sides, the equation is -2/3x=-2.
B.) After adding 4 to both sides, the equation is -2/3x=-10 .
C.) The equation can be solved for x using exactly one more step by multiplying both sides by -3/2.
D.) The equation can be solved for x using exactly one more step by dividing both sides by -2/3.
E.) The equation can be solved for x using exactly one more step by multiplying both sides by -2/3.
Given equation:
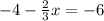
To show the steps we will carry out in order to solve for

Solution:
Solving for

Step 1:
Adding both sides by 4
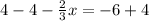
Thus, we get:
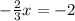
Thus statement A is correct.
Step 2:
Multiplying both sides by
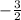
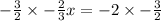
Thus, we get:
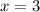 [Two negatives multiply to give a positive]
[Two negatives multiply to give a positive]
This proves that statement C is correct.
Or Step 2:
Dividing both sides by

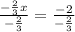
Thus, we get:
 [On dividing with a fractional divisor, we take reciprocal and multiply it with the dividend.]
[On dividing with a fractional divisor, we take reciprocal and multiply it with the dividend.]
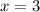 [Two negatives multiply to give a positive]
[Two negatives multiply to give a positive]
This prove that statement D is correct.