Question

The sum of a digit of a two digit number is 11. When the numbers reversed the new number is 27 less than the original number. Find the original number

Answer 1

`Original\ number = 74`

Explanation:

Let x be the 10's digit and y be the units digit.

So the original number is
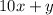`10x + y` and its reversed number is
`10y + x`

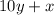
Given:

From the given statement the sum of the two digit is 11.

`x+y=11`

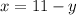`x=11-y` -------------------(1)

When the numbers reversed the new number is 27 less than the original number.

`(10x+y)-(10y+x)=27`

`10x+y-10y-x=27`

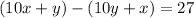
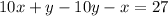
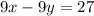`9x-9y=27`---------------(2)

Now we substitute x value in equation 2 from equation 1.

`9(11-y)-9y=27`

`99-9y-9y=27`

`99-18y=27`

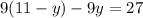
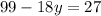
Now we add +18y both side in above equation.

`99-18y+18y=27+18y`

`99=27+18y`

`99-27=18y`

`99-27=18y`

`72=18y`

`y=(72)/(18)`

`y=4`

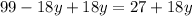
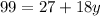
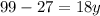
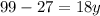
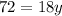
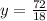
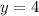
Now we substitute y = 4 in equation 1.

`x=11-4`

`x=7`

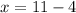
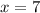
So the original number is
`10x+y = 10* 7 + 4=70+4=74`.

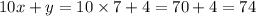Therefore the original number is 74.