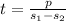Question

Given the equation p = s Subscript 1 Baseline t minus 2 Subscript 2 Baseline t, which equation is solved for t? t = p (s Subscript 1 Baseline minus s Subscript 2 Baseline) t = p minus s Subscript 1 Baseline minus s Subscript 2 t = StartFraction p Over s Subscript 1 Baseline minus s Subscript 2 Baseline EndFraction t = StartFraction p Over s Subscript 1 Baseline + s Subscript 2 Baseline EndFraction

A. t = p (s Subscript 1 Baseline minus s Subscript 2 Baseline)
B. t = p minus s Subscript 1 Baseline minus s Subscript 2
C. t = StartFraction p Over s Subscript 1 Baseline minus s Subscript 2 Baseline EndFraction
D. t = StartFraction p Over s Subscript 1 Baseline + s Subscript 2 Baseline EndFraction

Answer 1

C. t = StartFraction p Over s Subscript 1 Baseline minus s Subscript 2 Baseline EndFraction

Explanation:

Answer 2

Option C) is correct

That is t=StartFraction p Over s Subscript 1 Baseline minus s Subscript 2 Baseline EndFraction

It also can be written as
`t=(p)/(s_(1)-s_(2))`

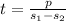
Explanation:

Given equation can be written as below:

`p=s_(1)t-s_(2)t`

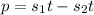
Now to solve the equation for t:

`p=s_(1)t-s_(2)t`

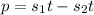
Taking common term t outside on RHS we get

`p=(s_(1)-s_(2))t`

`(p)/(s_(1)-s_(2))=t`

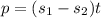
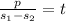
Rewritting the above equation as below

`t=(p)/(s_(1)-s_(2))`

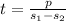
Therefore option C) is correct

That is t=StartFraction p Over s Subscript 1 Baseline minus s Subscript 2 Baseline EndFraction

It also can be written as
`t=(p)/(s_(1)-s_(2))`