Answer:
Graph of a cubic polynomial that falls to the left and rises to the right with x intercepts negative 1, 1, and 4. The graph intersects the y axis at a point between 0 and 5.
Explanation:
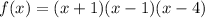
The x-intercepts are when
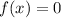
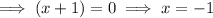
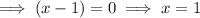
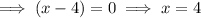
Therefore, the x-intercepts are -1, 1 and 4
The y-intercept is when
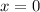
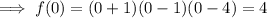
Therefore, the graph intersects the y-axis at (0, 4)
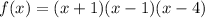
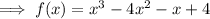
As the degree of the polynomial is odd (3 = cubic) and the leading coefficient is positive, the end behavior of the function is:
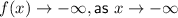
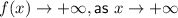
So this graph falls to the left and rises to the right.