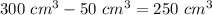Question

Type the correct answer in the box.

12 cm
5 cm
5 cm
A rectangular prism has a height of 12 centimeters and a square base with sides measuring 5 centimeters. A pyramid with the same base and
half the height of the prism is placed inside the prism, as shown in the figure.
The volume of the space outside the pyramid but inside the prism is
cubic centimeters.
imentum. All rights reserved.

Answer 1

`250\ cm^3`

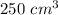
Explanation:

step 1

Find the volume of the prism

The volume of the prism is equal to

`V=LWH`

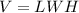
we have

`L=5\ cm\\W=5\ cm\\H=12\ cm`

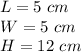
substitute

`V=(5)(5)(12)=300\ cm^3`

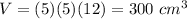
step 2

Find the volume of the pyramid

The volume of the pyramid is

`V=(1)/(3)Bh`

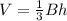
where

B is the area of the base

`B=5^2=25\ cm^2`

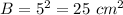
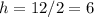`h=12/2=6\cm` ---> half the height of the prism

substitute

`V=(1)/(3)(25)(6)=50\ cm^3`

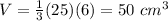
step 3

we know that

The volume of the space outside the pyramid but inside the prism is equal to subtract the volume of the pyramid from the volume of the cylinder

`300\ cm^3-50\ cm^3=250\ cm^3`