first off, let's notice something, we are using < or less than, which means our line will be a dashed line, meaning it will not include points at the borderline, and after that, let's then graph the line for y = (4/5)x + 3, the EQUATion equivalent.
we'll do a true/false check on the regions of the line, to see which region gets shaded, namely which one is the "true" region.
well, let's try say hmmm point (0,0) where x = 0 and y = 0, let's check that
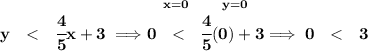
now hmmmm is 0 really less than 3? is that really true? yeap, 0 is indeed smaller than 3, that means that the (0,0) point lies on the "true" region, and that's the one we'll shade.
Check the picture below.