Question

Please help me with these problems.

Answer 1

15. The numbers 3,-6, 12, -24,...

16. The numbers -3, -1,5, 23,...

17, The numbers 3, 9, 15, 21,...

18.
`\sum_(n=1)^(\infty) 4((1)/(2))^(n-1)`

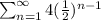
19. The sum is 8

20.
`a_(10)=-12`

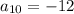
Explanation:

Question 15:

For the recursive sequence
`a_1=3, a_n=a_(n-1)*(-2)`

`a_1=3,\\a_2=3(-2)=-6\\a_3=-6(-2)=12\\a_4=12(-2)=-24`

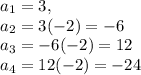
Therefore we get the numbers: 3, -6, 12, -24, ...

Question 16:

For the sequence
`a_n=3^(n-1)-4`

`a_1=-3\\a_2=-1\\a_3=5\\a_4=23`

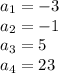
Therefore we have the numbers -3, -1, 5, 23, ....

Question 17.

For the recursive equation
`a_n=a_(n-1)+6`

`a_1=3`

`a_2=3+6=9`

`a_3=9+6=15`

`a_4=15+6=21`

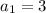
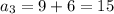
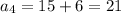
The numbers generated are 3, 9, 15, 21,...

Question 18.

In the series
`(4,2,1,(1)/(2),... )`

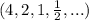
each following number is
`(1)/(2)` the previous number. The first term is 4, and the sequence has infinite terms; therefore, we have

`\sum_(n=1)^(\infty) 4((1)/(2))^(n-1)`

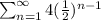
Question 19.

`\sum_(n=1)^(\infty) 4((1)/(2))^(n-1)=4*\sum_(n=1)^(\infty) ((1)/(2))^(n-1)`

since

`\sum_(n=1)^(\infty) ((1)/(2))^(n-1)=1-(1)/(2^(n-1))`

as n approaches infinity

`\lim_(n \to \infty) 1-(1)/(2^(n-1))=1`

therefore we have

`\sum_(n=1)^(\infty) 4((1)/(2))^(n-1)=4*\sum_(n=1)^(\infty) ((1)/(2))^(n-1)=4*1=4`

`\boxed{\sum_(n=1)^(\infty) 4((1)/(2))^(n-1)=4}`

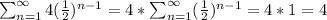
The sum is 4.

Question 20.

an arithmetic sequence has the form

`a_n=a_1+(n-1)d`

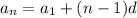
In our case
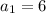`a_1=6` and
`d=-2`; therefore we have

`a_n=6-2(n-1)`

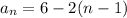
The 10th term of this sequence would be

`a_(10)=6-2(10-1)=6-2(9)=-12`

`\boxed{a_(10)=-12}`