Answer:
In the pile there are 10 quarters and 3 nickels.
Explanation:
Given:
Total amount of money = $2.65
Let number of nickels be 'n'.
Also Let number of quarters be 'd'
Now we now that;
nickels 'n' =$0.05
Quarters 'q' = $0.25
So the equation can be framed as;

Now Given:
there are 7 more quarters than nickels.
So we can say that;
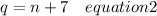
Now Substituting equation 2 in equation 1 we get;
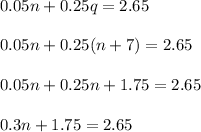
Now Subtracting both side by 1.75 using subtraction property of equality we get;
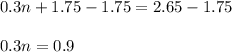
Now Dividing both side by 0.3 using division property of Inequality we get;
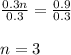
Now Substituting the value of n in equation 2 we get;
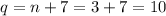
Hence In the pile there are 10 quarters and 3 nickels.