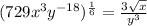Answer:
1) Option A) is correct
The given rational exponent expression is not simplified correctly as a radical expression is
![x^{(7)/(4)}=\sqrt[7]{x^4}](https://img.qammunity.org/2021/formulas/mathematics/high-school/irs51noodotf4jeeww3n3x4otyz5rniqyw.png)
2)Option A) is correct
That is
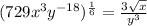
Explanation:
1) Given that
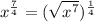
![x^{(7)/(4)}=\sqrt[4]{x^7}](https://img.qammunity.org/2021/formulas/mathematics/high-school/6prwp0v786xmjvii6qszo4w1fhqnud9kjb.png) is the correct answer but in the given problem they gave the RHS as wrong.
is the correct answer but in the given problem they gave the RHS as wrong.
Therefore the given rational exponent expression is not simplified correctly as a radical expression is
![x^{(7)/(4)}=\sqrt[7]{x^4}](https://img.qammunity.org/2021/formulas/mathematics/high-school/irs51noodotf4jeeww3n3x4otyz5rniqyw.png)
2)Given that the rational exponent expression is
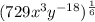
To find it as a radical expression:
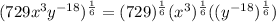
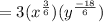
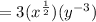
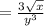
Therefore
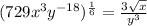
Therefore Option A) is correct
That is