Answer:
Radius of the convergence is R =
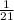
and,
The Interval of convergence is

Explanation:
Given function : Σ(21x)^k
Now,
Using the ratio test, we have
R =
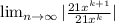
or
R =

or
R =
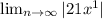
now,
for convergence R|x| < 1
Therefore,
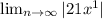 < 1
< 1
or

and,
Radius of the convergence is R =
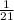
and,
The Interval of convergence is
