Question

A 12 kg crate, resting on a horizontal surface, is pulled by a force that is applied at an angle of 30° above the horizontal. Find the minimum force needed to start the crate moving if the coefficient of static friction is 0.40.

Answer 1

70.6N

Step-by-step explanation:

We are given that

Mass of crate=12 kg

`\theta=30^(\circ)`

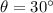
Coefficient of static friction=[tex\mu=[/tex]0.40

Horizontal component force is equal to friction force

`Fcos\theta=f=\mu N`

Force along vertical direction

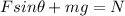`Fsin\theta+mg=N`..(2)

Using equation(2) in equation (1)

`Fcos\theta=\mu(Fsin\theta+mg)`

`Fcos\theta=\mu Fsin\theta+\mu mg`

`\mu mg=Fcos\theta-\mu Fsin\theta=F(cos\theta-\mu sin\theta)`

`F=(\mu mg)/(cos\theta-\mu sin\theta)`

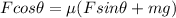
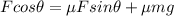
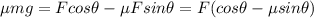
Substitute the values then we get

`F=(2* 0.40* 9.8)/(cos 30-0.40sin 30)`

`F=70.6N`

Hence, the minimum force needed to start the crate moving=70.6N