Question

Please help me wit dis no one would help and i really need help

Please don’t say anything unhelpful

Answer 1

(4) 64 tiles, (5)
`\mathrm{N}=\mathrm{s}^(2)`, (6)
`N^(2)=S^(4)`

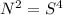
Explanation:

Given data: Side length of square tile = 1 ft

(4) Side length of square pool = 8 ft

`\text {Number of tiles} =\frac{\text { Area of square pool }}{\text { area of square tile }}`

`=(8 * 8)/(1 * 1)`

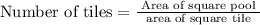
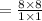
= 64

Hence 64 tiles needed for the border.

(5) Suppose number of square tiles be N and side of square tub is s ft.

So, N =
`(s * s)/(1 * 1)`

`\Rightarrow N=s^(2)`

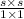
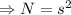
So, the expression is
`\mathrm{N}=\mathrm{s}^(2)`.

(6) The equivalent expression is
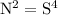`\mathrm{N}^(2)=\mathrm{S}^(4)`.