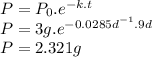Question

The half-life of phosphorus-32 is approximately 24.3 days. How much of a 3 gram sample of phosphorus-32 would remain after 9 days? Round to three decimal places.

Answer 1

2.321 g

Explanation:

The half-life (t1/2) of phosphorus-32 is approximately 24.3 days. We can calculate the rate constant (k) using the following expression.

k = ln2 / t1/2 = ln2 / 24.3 d = 0.0285 d⁻¹

We have an initial amount of ³²P of 3 grams (P₀=3g). After a time t = 9 days, the mass remaining (P) can be calculated using the following expression.

`P=P_(0).e^(-k.t) \\P=3g.e^{-0.0285d^(-1) .9d}\\P=2.321g`