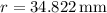Question

The volume of an inflated spherical water balloon is 176,868 mm3. What is the radius of the inflated water balloon?

Answer 1

51 mm

Explanation:

Answer 2

the radius of the inflated balloon is:
`r=34.822\,\text{mm}`

Explanation:

Since it is stated that the water balloon has a spherical shape: We can confidently use the formula for the volume of a sphere to calculate the radius.

Volume is denoted as 'V' and radius is denoted as 'r'.

`V=(4)/(3)\pi r^3`

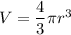
Volume is 176,868 mm^3

`176868=(4\pi r^3)/(3)`

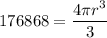
Now we can solve for the radius r.

`(3)/(4\pi)(176868)=r^3`

`(3(176868))/(4\pi)=r^3`

`(132651)/(\pi)=r^3`

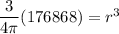
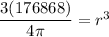
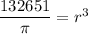
cube root both sides

`\sqrt[3]{(132651)/(\pi)}=\sqrt[3]{r^3}`

`r= \frac{51}{\sqrt[3]{\pi}}\approx34.822\,\text{mm}`

the radius of the inflated balloon is:
`r=34.822\,\text{mm}`