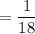Question

You roll two fair dice, one green and one red.

(a) Are the outcomes on the dice independent?

i. Yes
ii. No
(b) Find P(5 on green die and 3 on red die). (Enter your answer as a fraction.)
(c) Find P(3 on green die and 5 on red die). (Enter your answer as a fraction.)
(d) Find P((5 on green die and 3 on red die) or (3 on green die and 5 on red die)). (Enter your answer as a fraction.)

Answer 1

Answer: a) i. Yes

b)
`(1)/(36)`

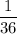
c)
`(1)/(36)`

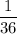
d)
`(1)/(18)`

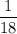
Explanation:

a) If we roll two different dice , then the outcomes on the dice are independent of each other.

So , if we roll two fair dice, one green and one red. , then the outcomes on the dice are independent.

Therefore , correct answer is "Yes".

b) Total outcomes on each die = 6 (1,2,3,4,5,6)

`Probability=(Favorable \ outcomes)/(Total \ outcomes)`

`P(\text{5 on green die })=(1)/(6)`
`P(\text{3 on red die })=(1)/(6)`

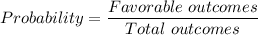
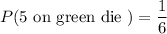
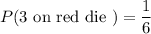
If any two event E and F are independent , then P(E and F)= P(E) x P(F)

P(E or F)= P(E)+P()

Find P(5 on green die and 3 on red die) = P(5 on green die) x P(3 on red die)

`=(1)/(6)*(1)/(6)=(1)/(36)`

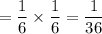
So ,P(5 on green die and 3 on red die)
`=(1)/(36)`

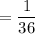
c) P(3 on green die and 5 on red die) = P(3 on green die) x P(5 on red die)

`=(1)/(6)*(1)/(6)=(1)/(36)`

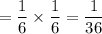
So ,P(3 on green die and 5 on red die)
`=(1)/(36)`

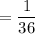
d) P((5 on green die and 3 on red die) or (3 on green die and 5 on red die))

= P(3 on green die and 5 on red die) + P(5 on green die and 3 on red die) (∵ Both are mutually exclusive.)

`=(1)/(63)+(1)/(36)=(2)/(36)=(1)/(18)`

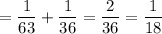
∴ P((5 on green die and 3 on red die) or (3 on green die and 5 on red die))

`=(1)/(18)`