Answer:
a) X that is a distribution of number of years of education for self-employed individuals.
b) Mean = 15.1, Standard Deviation = 0.8
c) Mean = 15.1, Standard Deviation = 0.4
Explanation:
We are given the following in the question:
The population distribution of number of years of education for self-employed individuals in a certain region has a mean of 15.1 and a standard deviation of 4.8
a) The random variable is X that is a distribution of number of years of education for self-employed individuals.
b) According to central limit theorem, as the sample size increases the distribution of means approaches a normal distribution.
Thus,
 has a normal distribution with
has a normal distribution with
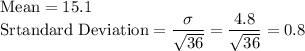
c) n = 144
 has a normal distribution with
has a normal distribution with
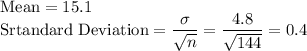
By increasing n, the standard deviation for distribution of mean reduced by one half. Therefore, we see that quadrupling the sample size will reduce the standard deviation by one half.