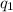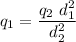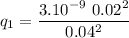Answer:
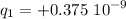
Step-by-step explanation:
Electrostatic Forces
The force exerted between two point charges
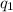 and
and
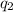 separated a distance d is given by Coulomb's formula
separated a distance d is given by Coulomb's formula
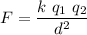
The forces are attractive if the charges have different signs and repulsive if they have equal signs.
The problem described in the question locates three point charges in a straight line. The charges have the values shown below
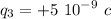
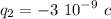
The distance between
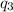 and
and
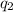 is
is
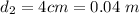
The distance between
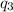 and
and
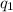 is
is
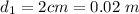
We must find the value of
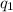 such that
such that

Applying Coulomb's formula for
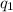 is
is
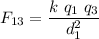
Now for
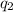
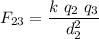
If the total force on
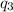 is zero, both forces must be equal. Note that being q2 negative, the force on q3 is to the right. The force exerted by q1 must go to the left, thus q1 must be positive. Equating the forces we have:
is zero, both forces must be equal. Note that being q2 negative, the force on q3 is to the right. The force exerted by q1 must go to the left, thus q1 must be positive. Equating the forces we have:
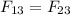
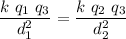
Simplfying and solving for